Loading...
Hypothesis Testing: Sign Test
What is a Sign Test?
A sign test is an inferential technique to assess two competing hypotheses about the population medians across one or two samples. We can use the sign test for three specific purposes:
One-Sample: This tests whether the population median is less than, greater than, or not equal to a prespecified value. The b statistic counts the number of observations greater than the median assumed in the null hypothesis, which states that the population median equals the testing value. The resulting p-value tells us how likely observing the evidence we have for the alternative hypothesis or more when the null hypothesis is true. If the p-value is less than the specified significance level (e.g., less than 0.05), we reject the null hypothesis in favor of the alternate hypothesis, which states that the population median is less than, greater than, or not equal to the testing value. Otherwise, we fail to reject the null hypothesis, indicating we do not have significant evidence for the alternative hypothesis.
Two Independent Samples: This tests whether the difference of two population medians is lesser, greater than, or not equal to a prespecified value, which we frequently take to be zero. The đÂČ statistic compares the observed data with what we expect under the null hypothesis, which states that the difference in population medians equals the testing value; usually, we take the testing value to be zero (e.g., the medians are the same). The resulting p-value tells us how likely observing the evidence we have for the alternative hypothesis or more when the null hypothesis is true. If the p-value is less than the specified significance level (e.g., less than 0.05), we reject the null hypothesis in favor of the alternate hypothesis, which states that the difference of population medians is less than, greater than, or not equal to the testing value. Otherwise, we fail to reject the null hypothesis, indicating we do not have significant evidence for the alternative hypothesis. This test is called Mood's median test, an extension of the sign test.
Paired Samples: This tests whether the population median of differences is lesser, greater than, or not equal to a prespecified value, which we frequently take to be zero. This procedure is used for a pre-post design. The b statistic compares the observed data with what we expect under the null hypothesis, which states that the population median of differences equals the testing value; usually, we take the testing value to be zero (e.g., the differences have a median of zero). The resulting p-value tells us how likely observing the evidence we have for the alternative hypothesis or more when the null hypothesis is true. If the p-value is less than the specified significance level (e.g., less than 0.05), we reject the null hypothesis in favor of the alternate hypothesis, which states that the population median difference is less than, greater than, or not equal to the testing value. Otherwise, we fail to reject the null hypothesis, indicating we do not have significant evidence for the alternative hypothesis.
The sign test can be used under the following conditions.
1. The observations are representative of the population of interest and independent.
2. The observations are continuous. The sign test is sensitive to data where there can be several observations at the assumed median, which can cause unreliable results.
How to use this app?
Step 1: To use this app, go to the 'Dataset & Hypothesis' tab and upload your .csv type dataset, or select a sample dataset.
Step 2: Next, you must select the type of sign-test (One-Sample, Two Independent Samples, or Paired Sample).
Step 3: You can check the assumptions in the 'Summary & Assumptions' tab.
Step 4: You can check the result of the selected hypothesis test procedure (test statistics, decision making, and test visualization) in the 'Hypothesis Test' and 'Confidence Interval' tabs.
Step 5 (Optional): We also provide the results of a bootstrap approach for computing a confidence interval and a randomization test. These are alternatives to the sign test that can be used to evaluate hypotheses about the data using resampling.
Contact us
Please contact us if you have any questions at datascience@colgate.edu.
Example 1
Within the sign test app, we provide the penguin data that includes measurements for penguin species inhabiting islands in Palmer Archipelago and made available through the palmerpenguins library for R (Gorman et al., 2014). Suppose researchers aimed to evaluate whether Adelie and Chinstrap penguins have differing bill depth (mm). This is a classic example of a scenario requiring the sign test framework.
Here, we have three samples of observations (the species) and a continuous attribute (bill depth). We will use the sign test procedure to evaluate whether the data support the claim that Adelie and Chinstrap penguins have different population median bill depths.
First, we load the sign test app. Second, we click 'Sample Data' to load the penguin data. Once the data are loaded, we select the quantitative variable (bill_depth_mm) and the categorical variable (species). Ensure that we have chosen the two-sample Mood's median test (independent), a two-sample extension of the sign test. Then we specify the independent samples as the Adelie and Chinstrap.
The first step of conducting the sign test procedure requires us to evaluate the assumptions. When we click 'Assumptions', a data summary provides our first look at the data.
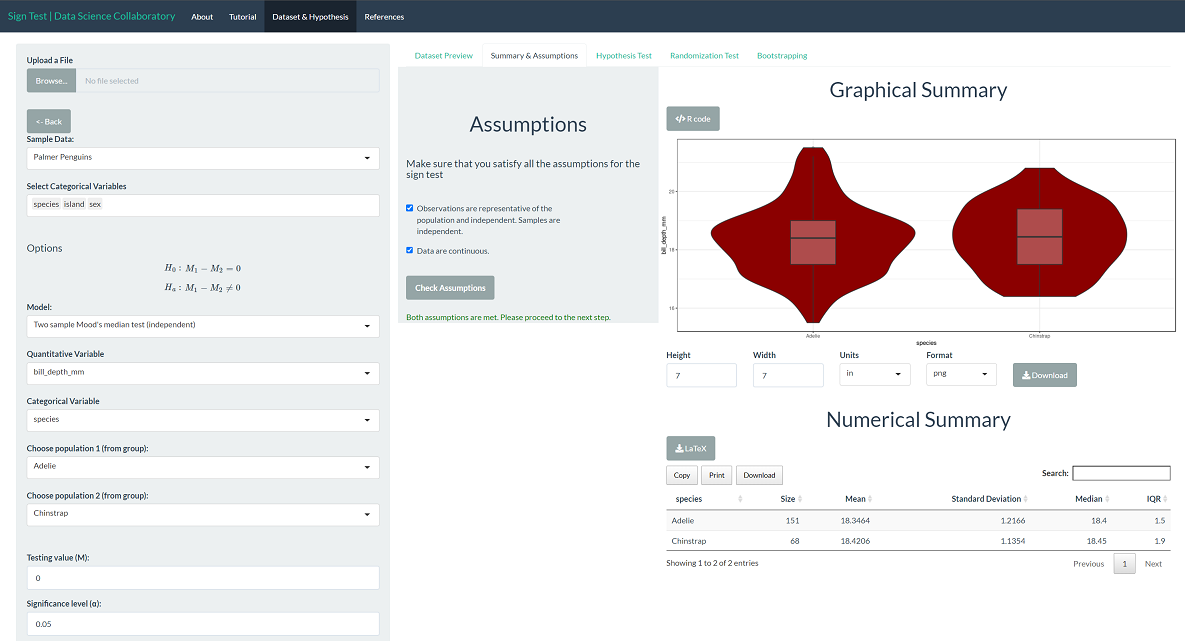
The bill depth (mm) is a continuous variable, making it suitable for Mood's median test. These data were collected from many penguin nests across three different islands in Palmer Archipelago, meaning the data are likely representative. We trust that the researchers collected data in a way that made the observations near independent.
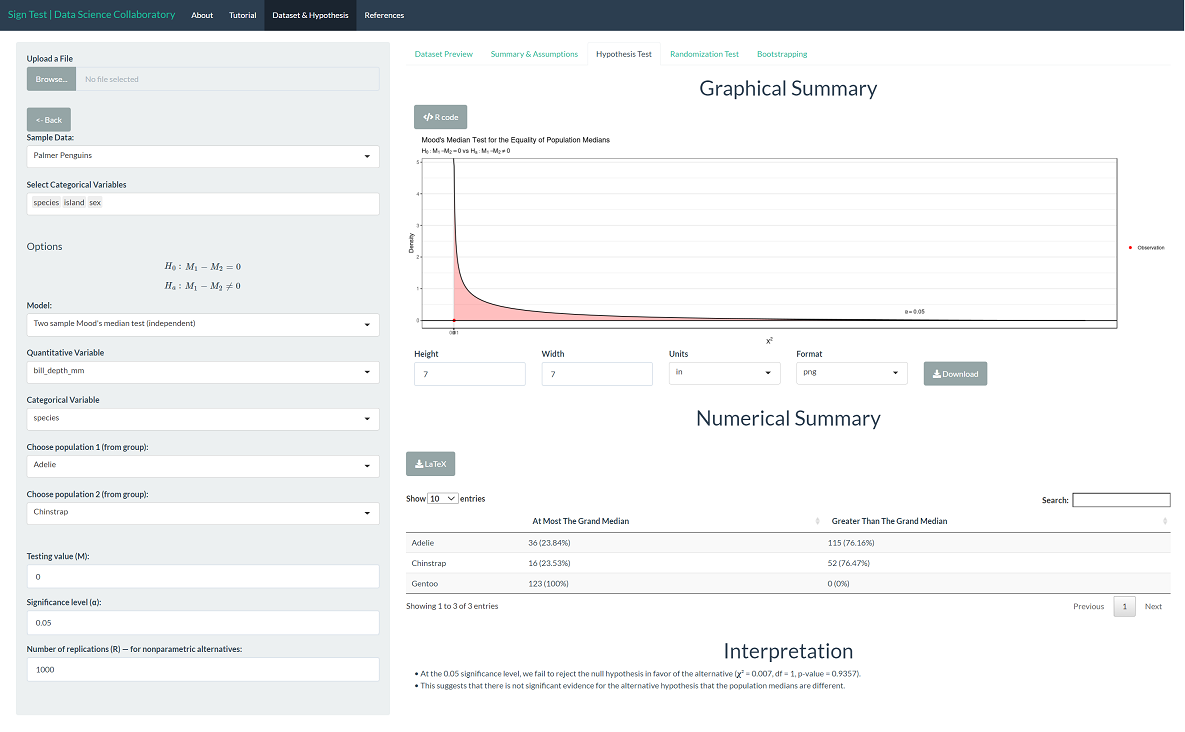
The 'Hypothesis Test' tab shows the result of Mood's median test. As we might expect after observing the plotted data, there is not significant evidence that the population median bill depths (mm) differ across Adelie and Chinstrap penguins (đÂČ=0.007, p=0.9357).
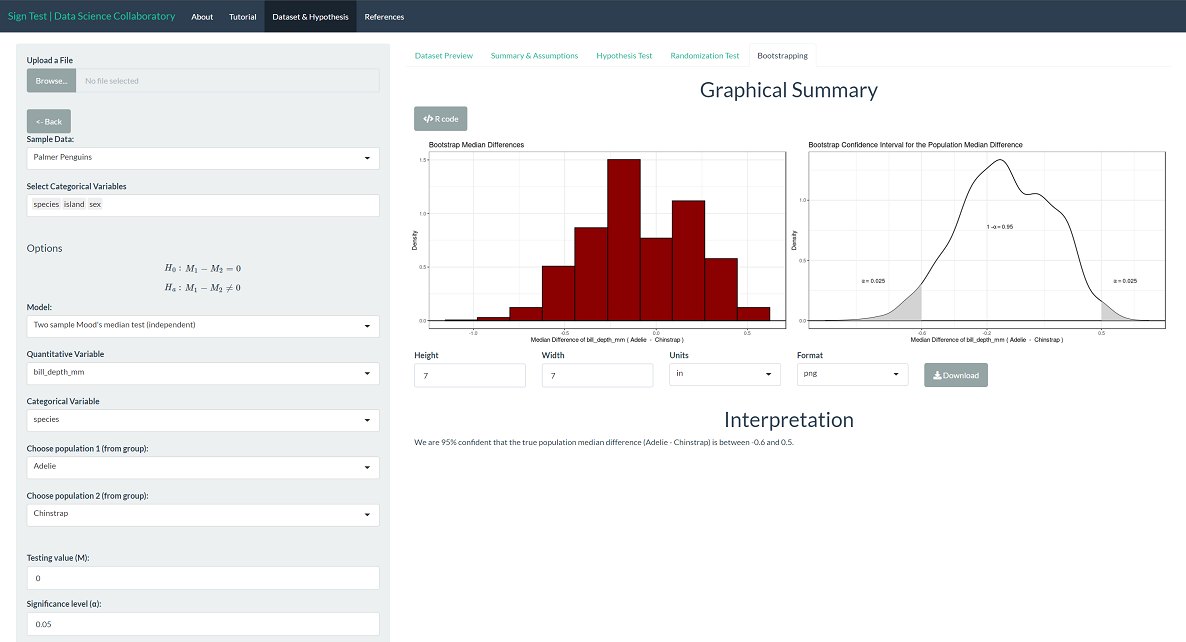
To provide context, we can interpret the corresponding boostrapping confidence interval for the population median difference. We are 95% confident that the true population median difference of bill depths (Adelie - Chinstrap) is between -0.60 mm and 0.50 mm. Note that zero is on this interval, indicating that it is plausible that the population medians are the same, which agrees with the interpretation of the test.
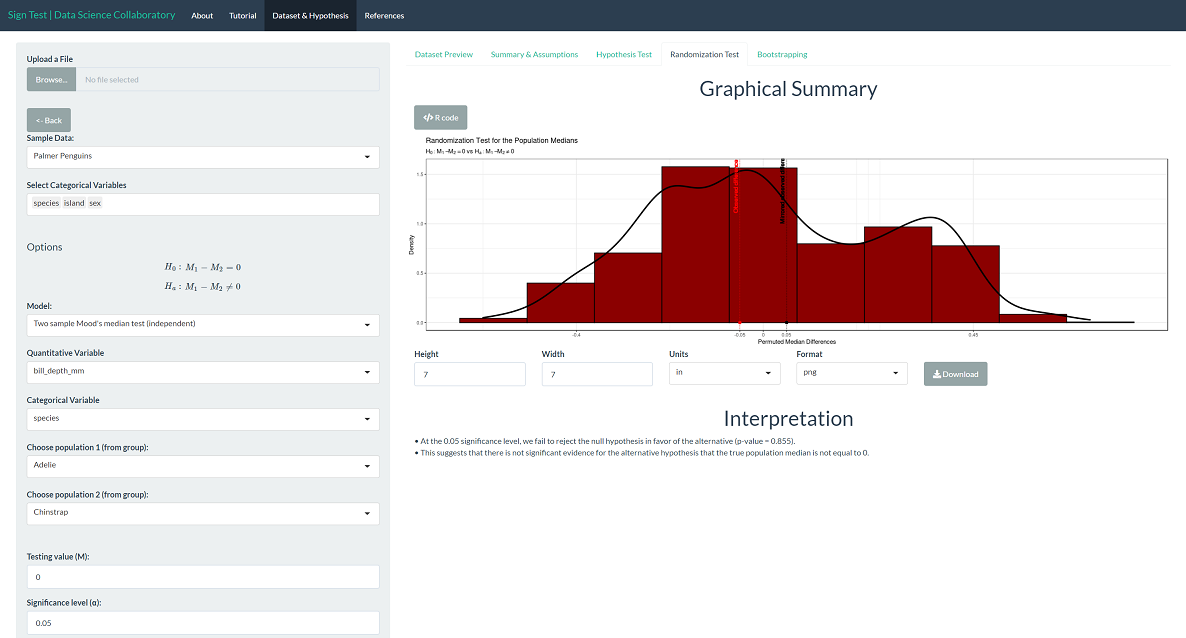
The randomization test produces results close to the sign test. Specifically, the randomization test produces a p-value of 0.855, which leads us to conclude that there is not significant evidence that the population median bill depths (mm) differ across Adelie and Chinstrap penguins. Note that this is the result of random resampling, and if you run the inference yourself, the result may vary slightly.
Gorman KB, Williams TD, Fraser WR (2014) Ecological Sexual Dimorphism and Environmental Variability within a Community of Antarctic Penguins (Genus Pygoscelis). PLoS ONE 9(3): e90081. doi:10.1371/journal.pone.0090081
Example 2
Within the sign test app, we provide the MFAP4 data, including measurements for Hepatitis C patients collected by the German network of Excellence for Viral Hepatitis and studied by Bracht et al. (2016). Suppose these researchers wanted to show that the human microfibrillar-associated protein 4 (MFAP4, U/ml) is increased for hepatitis C patients. The researchers can use the sign test to evaluate whether the population median log-2 transformed MFAP4 is greater than that of healthy patients, which we take to be 1.71 U/ml (Zhang et al., 2019) on the log-2 scale.
Here, we have one sample of observations and a continuous attribute (MFAP4 log-2 U/ml). We will use the sign test procedure to evaluate whether the data support the claim that the population median log-2 MFAP4 level in hepatitis C patients is larger than 1.71.
First, we load the sign test app. Second, we click 'Sample Data' to load the MFAP4 data. Once the data are loaded, we select the variable (log2.MFAP4).
The first step of conducting the sign test procedure requires us to evaluate the assumptions. When we click 'Assumptions', a data summary provides our first look at the data.
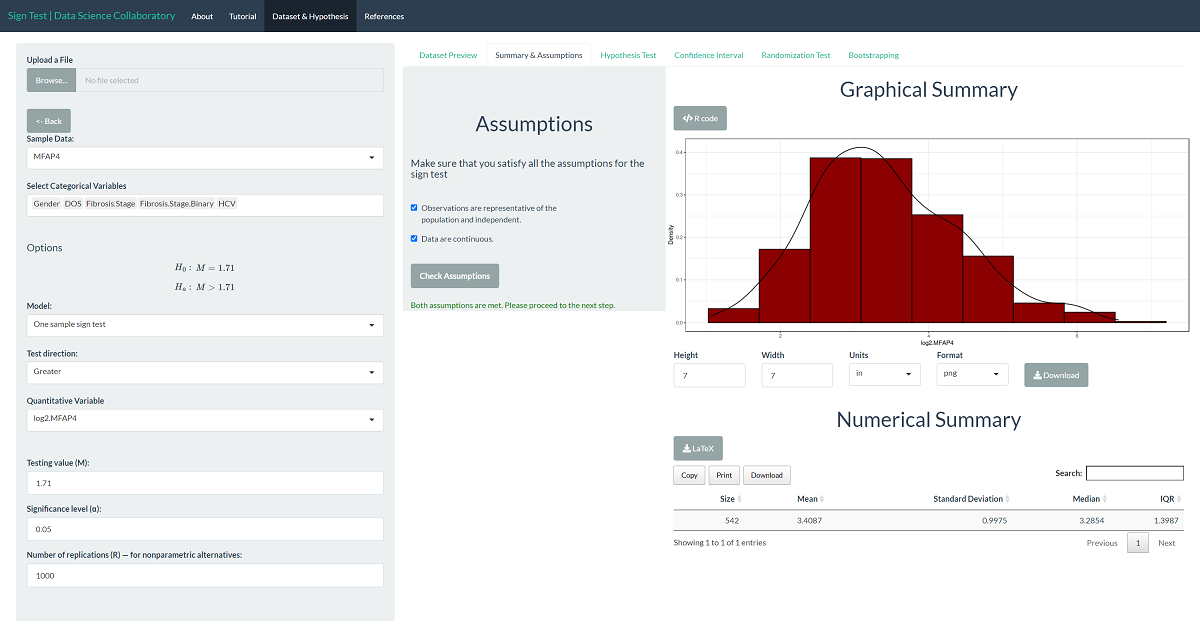
The log-2 MFAP4 U/ml is a continuous variable, making it suitable for the sign test. In their paper, Bracht et al. (2016) tell us these data were collected at different sites using a protocol meant to reduce bias, meaning the data are likely to be representative. We trust that the researchers collected data in a way that made the observations near independent.
The 'Hypothesis Test' tab shows the result of the sign test procedure. As we might expect after viewing graphs of the data, there is significant evidence that the population median MFAP4 U/ml level in hepatitis C patients is larger than 1.71 (b=530, p<0.0001).
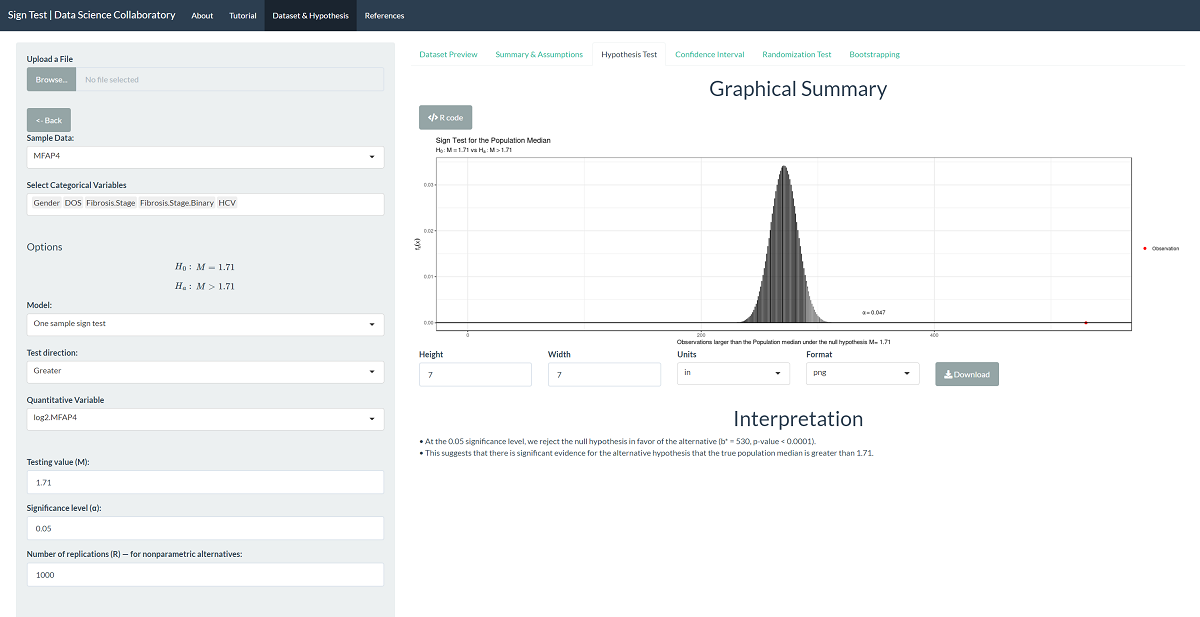
We can interpret the corresponding confidence interval for the population median to provide context. We are 95% confident that the true population median log-2 MFAP4 level of hepatitis C patients is between 3.2016 and 3.406 U/ml on the log-2 scale. Note that the values the interval covers are larger than 1.71, indicating that the population median log-2 MFAP4 level for hepatitis C patients is larger than 1.71.
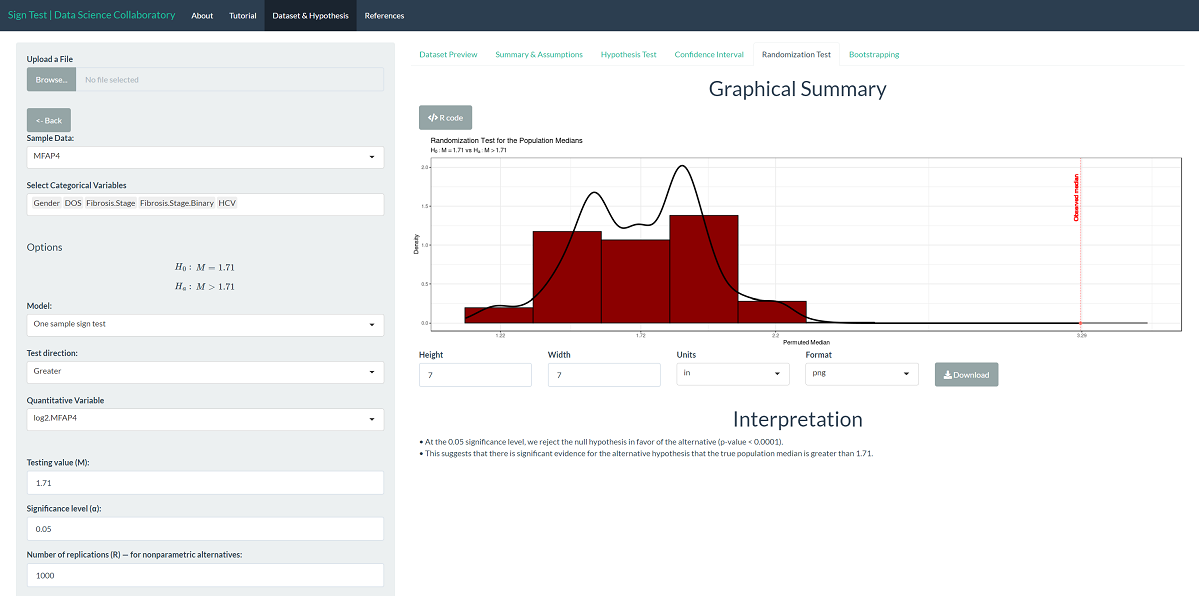
The randomization test produces results similar to the parametric result. Specifically, the randomization test produces a p-value < 0.0001, which leads us to conclude that there is significant evidence that the population median log-2 MFAP4 level is larger than 1.71. Note that this is the result of random sampling, and if you run the inference yourself, the result may vary slightly.
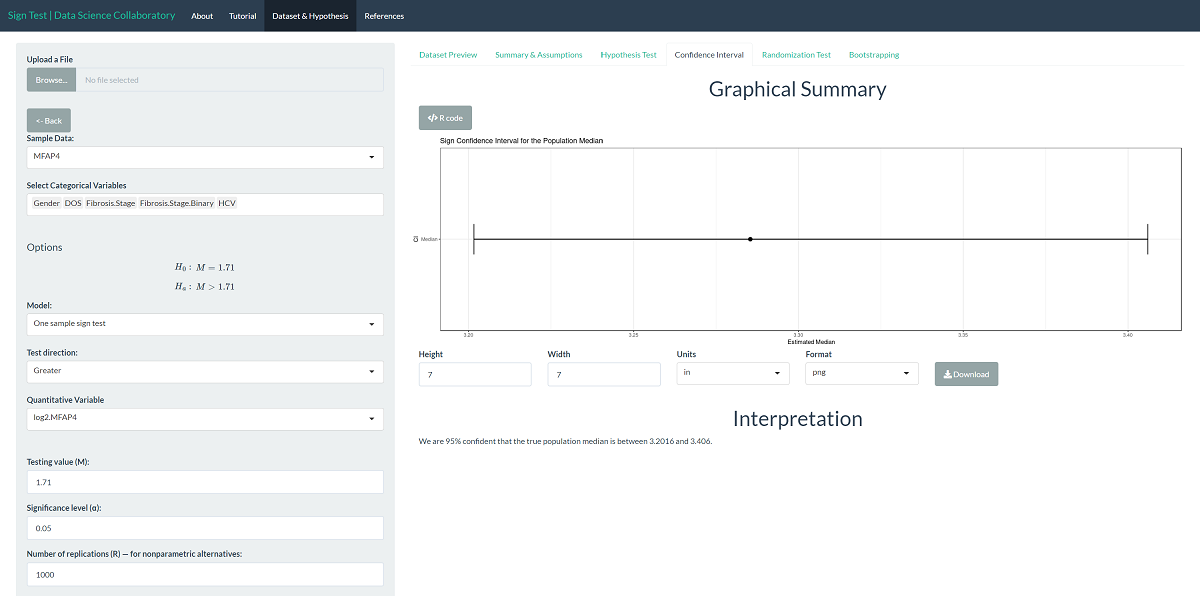
The same is true for the confidence interval. Using the bootstrap confidence interval, we are 95% confident that the true population median log-2 MFAP4 level among hepatitis C patients is between 3.2016 and 3.406. Note that this too is the result of random sampling, and if you run the inference yourself, the result may vary slightly.
Bracht, T., Molleken, C., Ahrens, M., Poschmann, G., Schlosser, A., Eisenacher, M., ... & Sitek, B. (2016). Evaluation of the biomarker candidate MFAP4 for non-invasive assessment of hepatic fibrosis in hepatitis C patients. Journal of Translational Medicine, 14(1), 1-9.
Zhang, X., Li, H., Kou, W., Tang, K., Zhao, D., Zhang, J., ... & Xu, Y. (2019). Increased plasma microfibrillar-associated protein 4 is associated with atrial fibrillation and more advanced left atrial remodelling. Archives of Medical Science, 15(3), 632-640.
Example 3
Within the sign test app, we provide U.S. News and World Report's College Data that includes measurements for many U.S. Colleges from the 1995 issue of U.S. News and World Report and made available through the ISLR library in R (James et al., 2017). Suppose we aimed to evaluate whether private schools have a higher percentage of new students coming from the top 10% of their high school class than public schools.
Here, we have two samples of observations (private/public) and a discrete attribute (percent of new students in the top 10% of their high school class). We will use Mood's median test to evaluate whether the data support the claim that there is a difference in the median percent of new students coming from the top 10% of their high school class.
First, we load the sign test app. Second, we click 'Sample Data' to load the U.S. News College data.
The first step of conducting the sign test procedure requires us to evaluate the assumptions. When we click 'Summary & Assumptions', we get our first look at the data.
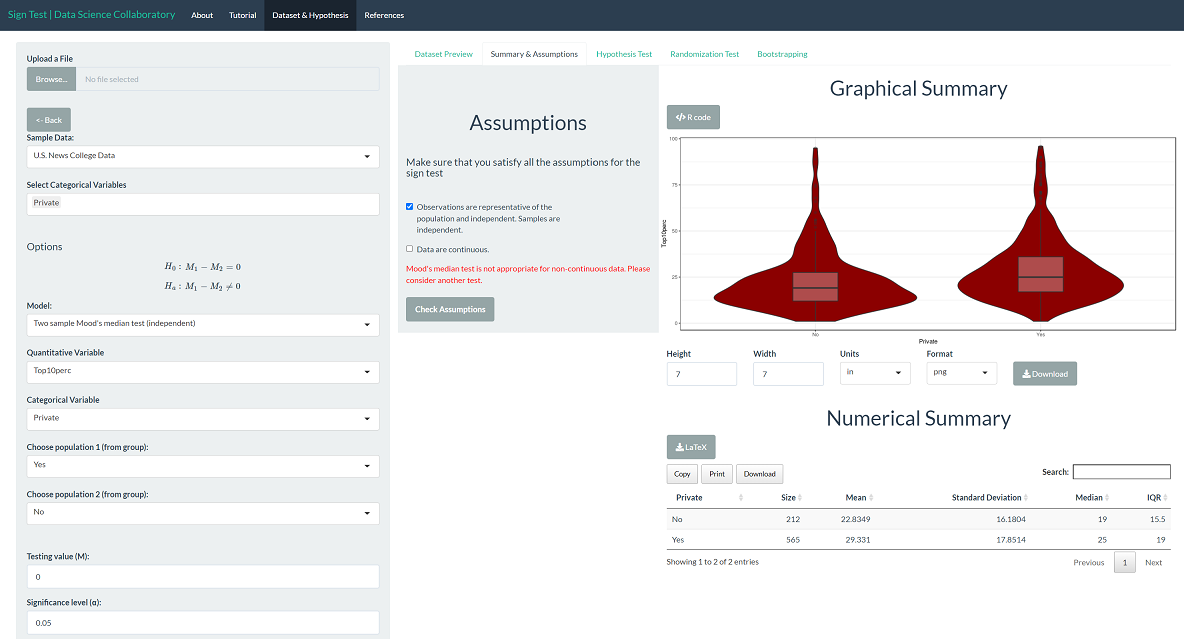
The percentage of new students in the top 10% of their high school class is a discrete variable. For any school, this percentage can only increase or decrease by 100/n, where n is the number of students enrolled. However, there are enough unique observations that there aren't many ties, so we proceed with caution. We won't get into how U.S. News conducts its ratings, but it has been heavily scrutinized in the media. For demonstration purposes, we will proceed assuming that the data are representative. The data may be representative, but we'd have to do more digging.
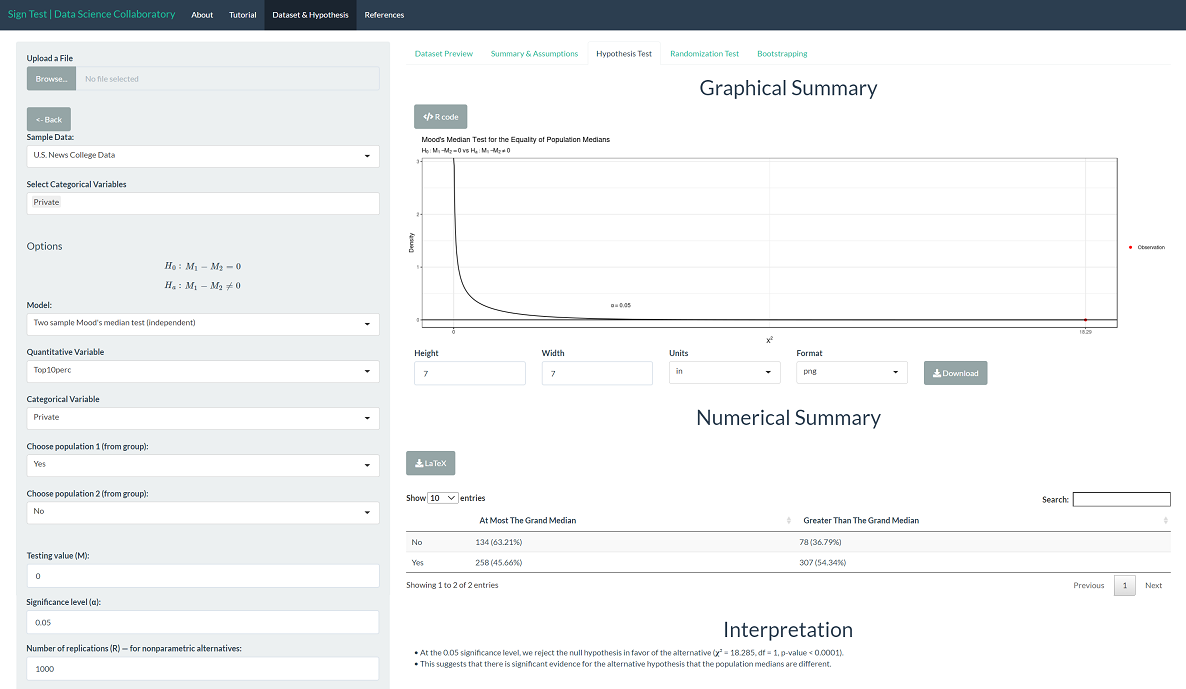
The 'Hypothesis Test' tab shows the result of the Mood's median test. As we might expect after viewing the data, there is significant evidence that the population median percentage of new students coming from the top 10% of their high school class differs across institution types (đÂČ=18.285, p < 0.0001).
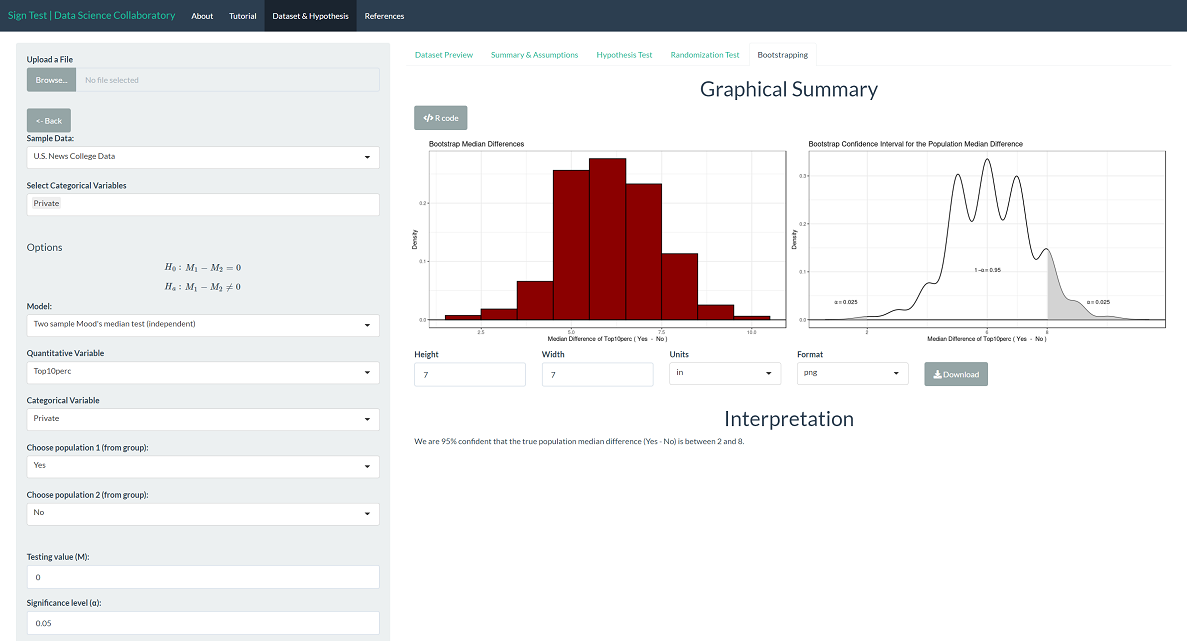
To provide context, we can interpret the corresponding bootstrap confidence interval for the population median difference. We are 95% confident that the true population median percentage of new students coming from the top 10% of their high school class (private-public) is between 2 and 8 percentage points. Note that the values the interval covers are larger than 0, indicating that the population median is larger for private schools than public schools.
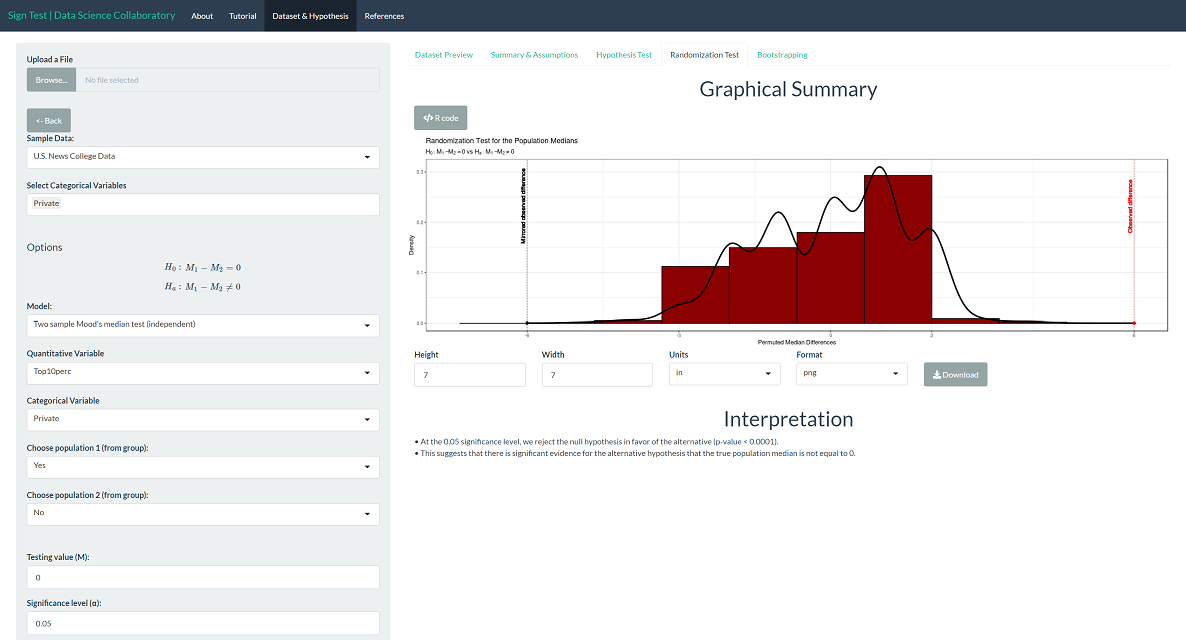
The randomization test produces a p-value < 0.0001, which leads us to the same conclusion as Mood's median test. Note that this is the result of random sampling, and if you run the inference yourself, the result may vary slightly.
Gareth James, Daniela Witten, Trevor Hastie and Rob Tibshirani (2017). ISLR: Data for an Introduction to Statistical Learning with Applications in R. R package version 1.2. https://CRAN.R-project.org/package=ISLR
Example 4
Within the sign test app, we provide the well-being data of undergraduate college students collected by Binfet et al. (2021). Suppose the researchers wanted to show that reported loneliness is decreased among undergraduate college students after contact with canines. The researchers can use the sign test to evaluate whether the population median loneliness is greater before canine contact than after. Loneliness is measured using the UCLA Loneliness Scale (Russell, 1996), the average of twenty questions answered on a one to four scale.
Here, we have two samples of observations (before/after) and a discrete attribute (self-reported loneliness). We will use the paired samples sign test to evaluate whether the population median loneliness is greater before canine contact than after.
First, we load the sign test app. Second, we click 'Sample Data' to load Binfet's Canine Data: Contact Group. Once the data are loaded, we select the `after' variable (lonely2) and the 'before' variable (lonely1). Ensure to choose Paired two-sample sign test (dependent).
The first step of conducting the sign test procedure requires us to evaluate the assumptions. When we click 'Assumptions', we get our first look at the data.
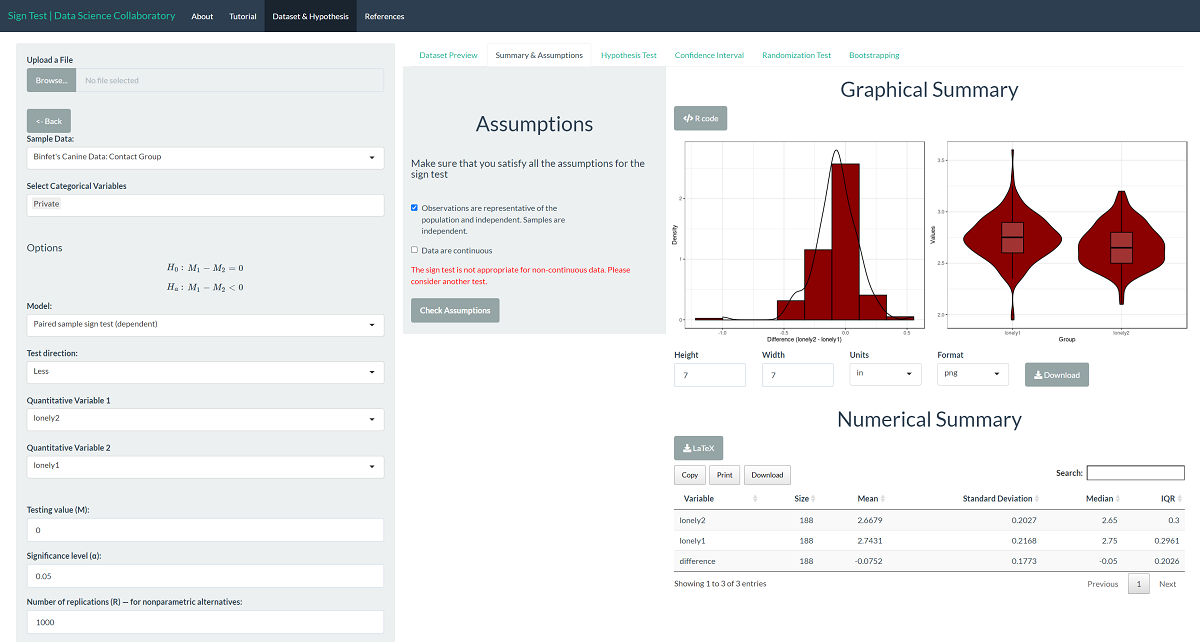
The loneliness score of participants is the average of twenty questions answered on a one to four scale, making it a discrete variable. For any participant, this score can only increase or decrease by 1/80, the difference in the average when adjusting one answer by 1. However, there are enough unique observations that there aren't many ties, so we proceed with caution. Binfet et al. (2021) recruited undergraduate students from one mid-sized Canadian University who were enrolled in a psychology course offering bonus credit for participating in research studies. While this sample may be representative of undergraduate students at midsized Canadian universities who take psychology courses, it may not represent all undergraduate students (e.g., non-Canadian institutions, students who don't take psychology courses, etc.).
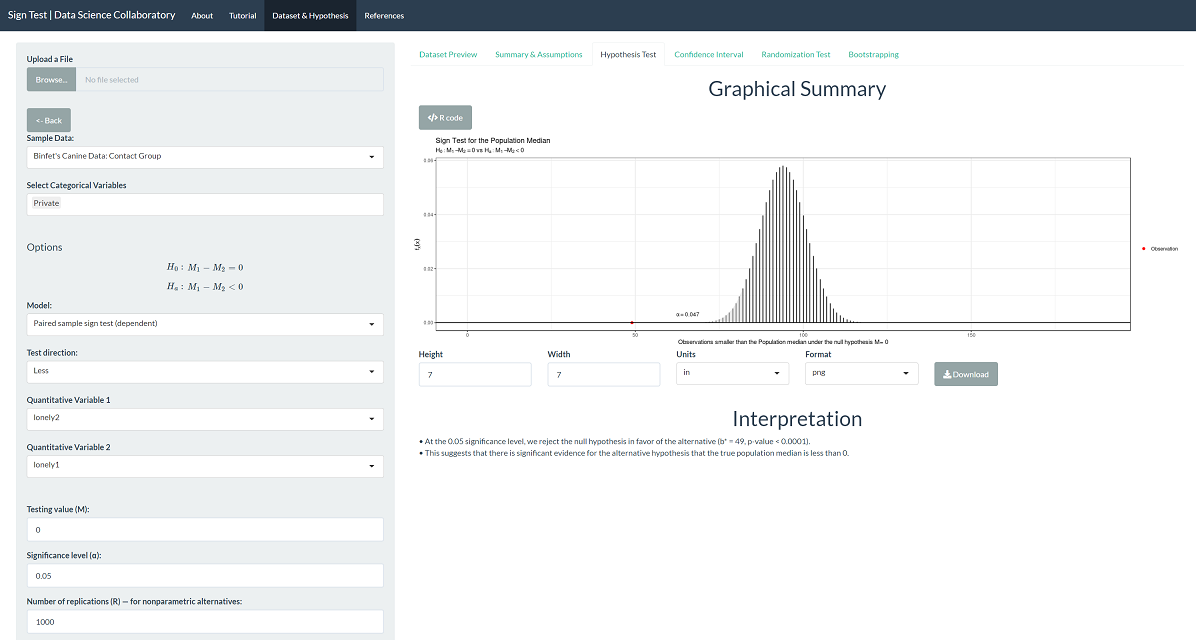
The 'Hypothesis Test' tab shows the result of the sign test procedure. There is significant evidence that the population median loneliness is greater before canine contact than after (b=49, p < 0.0001).
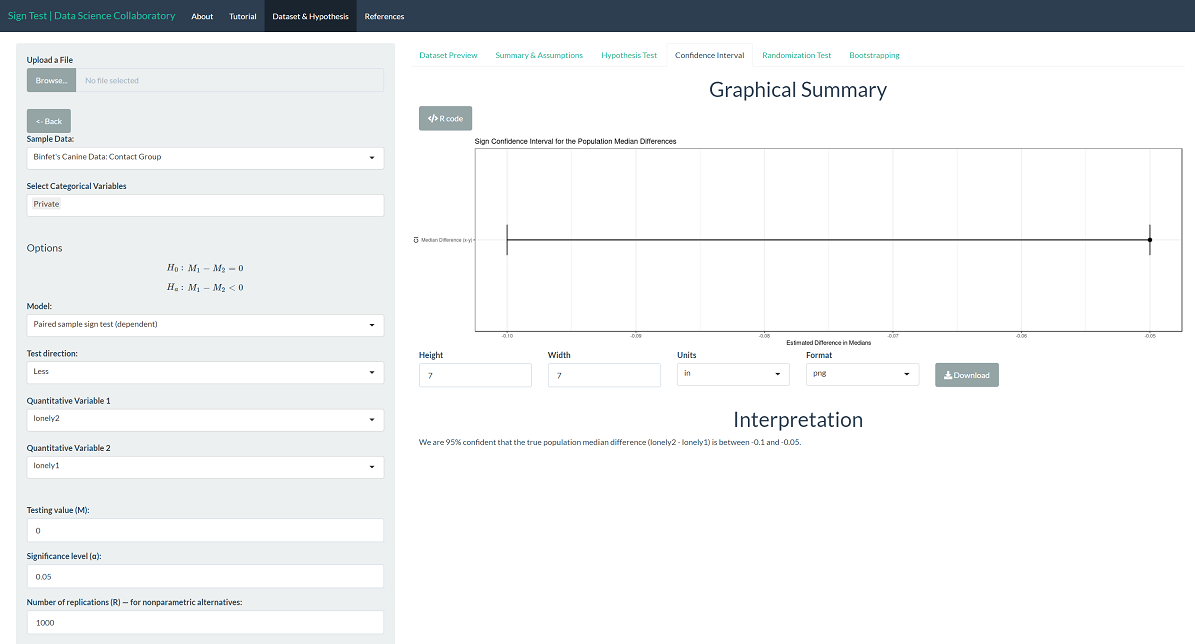
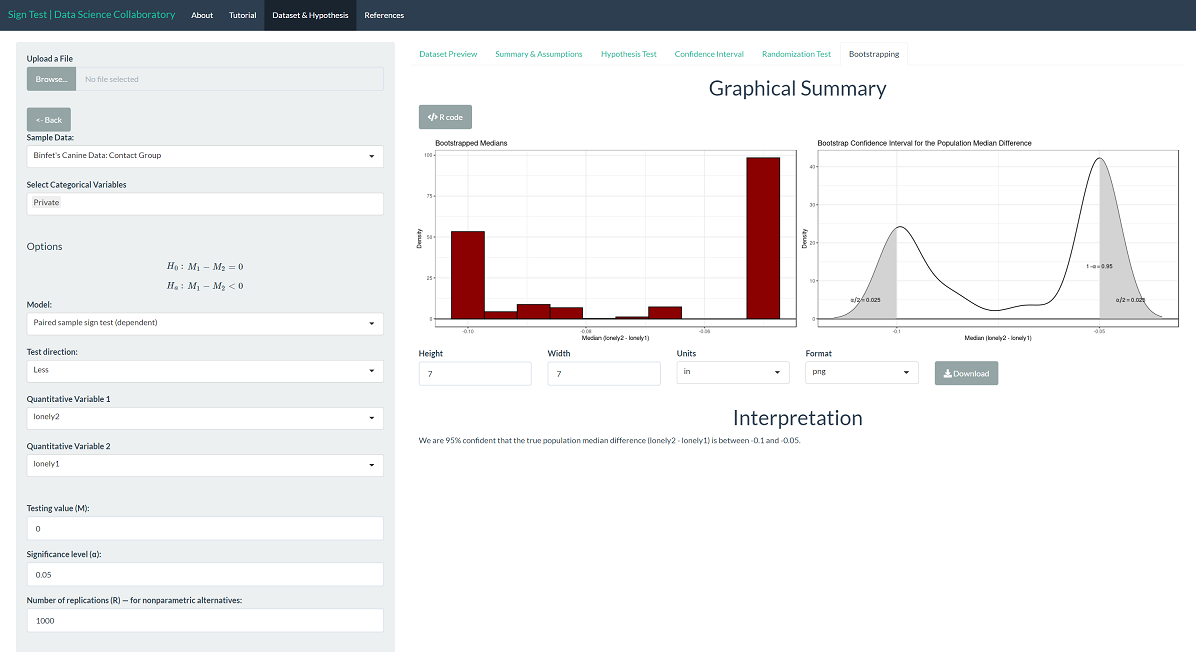
To provide context, we can interpret the corresponding confidence interval for the population median difference. We are 95% confident that the true population median loneliness (after-before) is between -0.1 and -0.05. Note that this difference is based on the average of responses on a 1 to 4 scale. That is, the difference is significant but not large. Note that the interval only covers values less than 0, indicating that the population median loneliness is larger before compared to after.
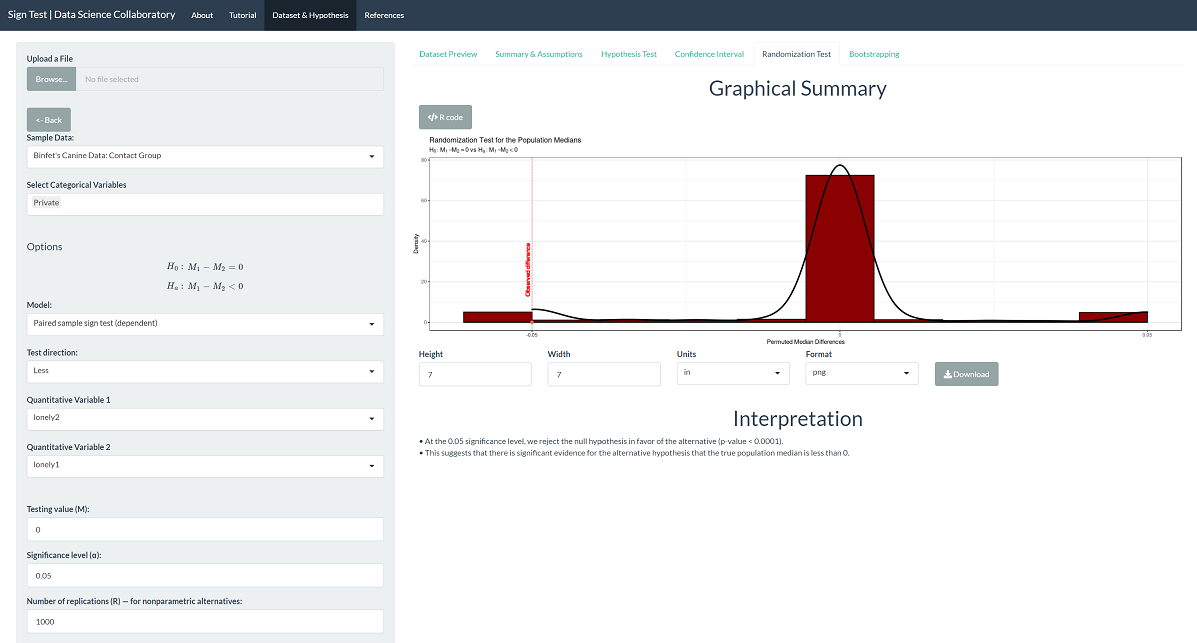
The randomization test produces a p-value < 0.0001, which leads us to the same conclusion. Note that this is the result of random sampling, and if you run the inference yourself, the result may vary slightly.
The same is true for the confidence interval. Using the bootstrap confidence interval, we are 95% confident that the true population median loneliness (after-before) is between -0.1 and -0.05. Note that this too is the result of random sampling, and if you run the inference yourself, the result may vary slightly.
Binfet, J. T., Green, F. L., & Draper, Z. A. (2022). The Importance of ClientâCanine Contact in Canine-Assisted Interventions: A Randomized Controlled Trial. Anthrozoös, 35(1), 1-22.
Russell, D. W. (1996). UCLA Loneliness Scale (Version 3): Reliability, validity, and factor structure. Journal of personality assessment, 66(1), 20-40.
References
Arnholt, Alan T., and Ben Evans. 2017. BSDA: Basic Statistics and
Data Analysis. https://CRAN.R-project.org/package=BSDA.
Attali, Dean. 2020. Shinyjs: Easily Improve the User Experience of
Your Shiny Apps in Seconds. https://deanattali.com/shinyjs/.
Attali, Dean, and Tristan Edwards. 2020. Shinyalert: Easily Create
Pretty Popup Messages (Modals) in Shiny. https://github.com/daattali/shinyalert
https:// daattali.com/shiny/shinyalert-demo/.
Bailey, Eric. 2015. shinyBS: Twitter Bootstrap Components for
Shiny. https://ebailey78.github.io/shinyBS.
Binfet, John-Tyler, Freya LL Green, and Zakary A Draper. 2021.
âThe Importance of ClientâCanine Contact in Canine-Assisted
Interventions: A Randomized Controlled Trial.â
Anthrozoös, 1â22.
Bracht, Thilo, Christian Mölleken, Maike Ahrens, Gereon Poschmann,
Anders Schlosser, Martin Eisenacher, Kai StĂŒhler, et al. 2016.
âEvaluation of the Biomarker Candidate Mfap4 for Non-Invasive
Assessment of Hepatic Fibrosis in Hepatitis c Patients.â
Journal of Translational Medicine 14 (1): 1â9.
Canty, Angelo, and Brian Ripley. 2021. Boot: Bootstrap Functions
(Originally by Angelo Canty for s). https://CRAN.R-project.org/package=boot.
Chang, Winston. 2021. Shinythemes: Themes for Shiny. https://rstudio.github.io/shinythemes/.
Chang, Winston, Joe Cheng, JJ Allaire, Carson Sievert, Barret Schloerke,
Yihui Xie, Jeff Allen, Jonathan McPherson, Alan Dipert, and Barbara
Borges. 2021. Shiny: Web Application Framework for r. https://shiny.rstudio.com/.
Cheng, Joe, and Carson Sievert. 2021. Shinymeta: Export Domain Logic
from Shiny Using Meta-Programming. https://CRAN.R-project.org/package=shinymeta.
Dahl, David B., David Scott, Charles Roosen, Arni Magnusson, and
Jonathan Swinton. 2019. Xtable: Export Tables to LaTeX or HTML.
http://xtable.r-forge.r-project.org/.
Davison, A. C., and D. V. Hinkley. 1997. Bootstrap Methods and Their
Applications. Cambridge: Cambridge University Press. http://statwww.epfl.ch/davison/BMA/.
Hervé, Maxime. 2021. RVAideMemoire: Testing and Plotting Procedures
for Biostatistics. https://CRAN.R-project.org/package=RVAideMemoire.
Horst, Allison, Alison Hill, and Kristen Gorman. 2020.
Palmerpenguins: Palmer Archipelago (Antarctica) Penguin Data.
https://CRAN.R-project.org/package=palmerpenguins.
James, Gareth, Daniela Witten, Trevor Hastie, and Rob Tibshirani. 2017.
ISLR: Data for an Introduction to Statistical Learning with
Applications in r. http://www.StatLearning.com.
Nijs, Vincent, Forest Fang, Trestle Technology, LLC, and Jeff Allen.
2019. shinyAce: Ace Editor Bindings for Shiny. https://CRAN.R-project.org/package=shinyAce.
Pedersen, Thomas Lin. 2020. Patchwork: The Composer of Plots.
https://CRAN.R-project.org/package=patchwork.
Peng, Roger D. 2019. Simpleboot: Simple Bootstrap Routines. https://github.com/rdpeng/simpleboot.
R Core Team. 2021. R: A Language and Environment for Statistical
Computing. Vienna, Austria: R Foundation for Statistical Computing.
https://www.R-project.org/.
Russell, Daniel W. 1996. âUCLA Loneliness Scale (Version 3):
Reliability, Validity, and Factor Structure.â Journal of
Personality Assessment 66 (1): 20â40.
Sali, Andras, and Dean Attali. 2020. Shinycssloaders: Add Loading
Animations to a Shiny Output While Itâs Recalculating. https://github.com/daattali/shinycssloaders.
Wickham, Hadley. 2021. Tidyverse: Easily Install and Load the
Tidyverse. https://CRAN.R-project.org/package=tidyverse.
Wickham, Hadley, Mara Averick, Jennifer Bryan, Winston Chang, Lucy
DâAgostino McGowan, Romain François, Garrett Grolemund, et al. 2019.
âWelcome to the tidyverse.â
Journal of Open Source Software 4 (43): 1686. https://doi.org/10.21105/joss.01686.
Xie, Yihui. 2014. âKnitr: A Comprehensive Tool for Reproducible
Research in R.â In Implementing Reproducible
Computational Research, edited by Victoria Stodden, Friedrich
Leisch, and Roger D. Peng. Chapman; Hall/CRC. http://www.crcpress.com/product/isbn/
9781466561595.
âââ. 2015. Dynamic Documents with R and Knitr. 2nd
ed. Boca Raton, Florida: Chapman; Hall/CRC. https://yihui.org/knitr/.
âââ. 2021. Knitr: A General-Purpose Package for Dynamic Report
Generation in r. https://yihui.org/knitr/.
Xie, Yihui, Joe Cheng, and Xianying Tan. 2021. DT: A Wrapper of the
JavaScript Library DataTables. https://github.com/rstudio/DT.
Zhang, Xianlin, Hailing Li, Wenxin Kou, Kai Tang, Dongdong Zhao,
Jingying Zhang, Jianhui Zhuang, et al. 2019. âIncreased Plasma
Microfibrillar-Associated Protein 4 Is Associated with Atrial
Fibrillation and More Advanced Left Atrial Remodelling.â
Archives of Medical Science 15 (3): 632â40.