Probability Calculator
What is a Probability Model?
A probability model is a function that describes the random behavior and properties of a random variable. This application supports various probability models of two types:
Discrete Probability Models describe discrete random variables, which have countable possible outcomes. This often means that we are counting; for example, we might count the number of times an event of interest occurs per week. Discrete probability models are defined by their probability mass function (PMF) which describes the probability of each possible outcome. A cumulative distribution function (CDF) is calculated from the PMF and returns the cumulative probability; e.g., P(X ≤ x).
Continuous Probability Models: describe continuous random variables, which have infinitely many possible outcomes. These observations are often made using units that can be made more precise. For example, we might report our age in years, months, weeks, days, hours, minutes, seconds, and so on. Continuous probability models are defined by their probability density function (PDF) which describes the likelihood of the possible outcomes. A cumulative distribution function (CDF) is calculated from the PDF and returns the cumulative probability; e.g., P(X ≤ x).
Each named distribution is described by a PMF/PDF, depending on whether the random variable it describes is discrete or continuous. The named distributions are indexed by a parameter or multiple parameters that determine the center, shape, and spread of the probability distribution.
How to use this app?
Step 1: To use this app, go to the 'Probability Calculator' tab.
Step 2: Next, you must select the named distribution and specify the necessary parameters.
Step 3: You can specify a probability of interest to calculate by selecting the appropriate expression, and specifying the necessary inputs.
Step 4: The resulting probability calculation is calculated and plotted and provided as output.
Contact us
Please contact us if you have any questions at datascience@colgate.edu.
Example 1
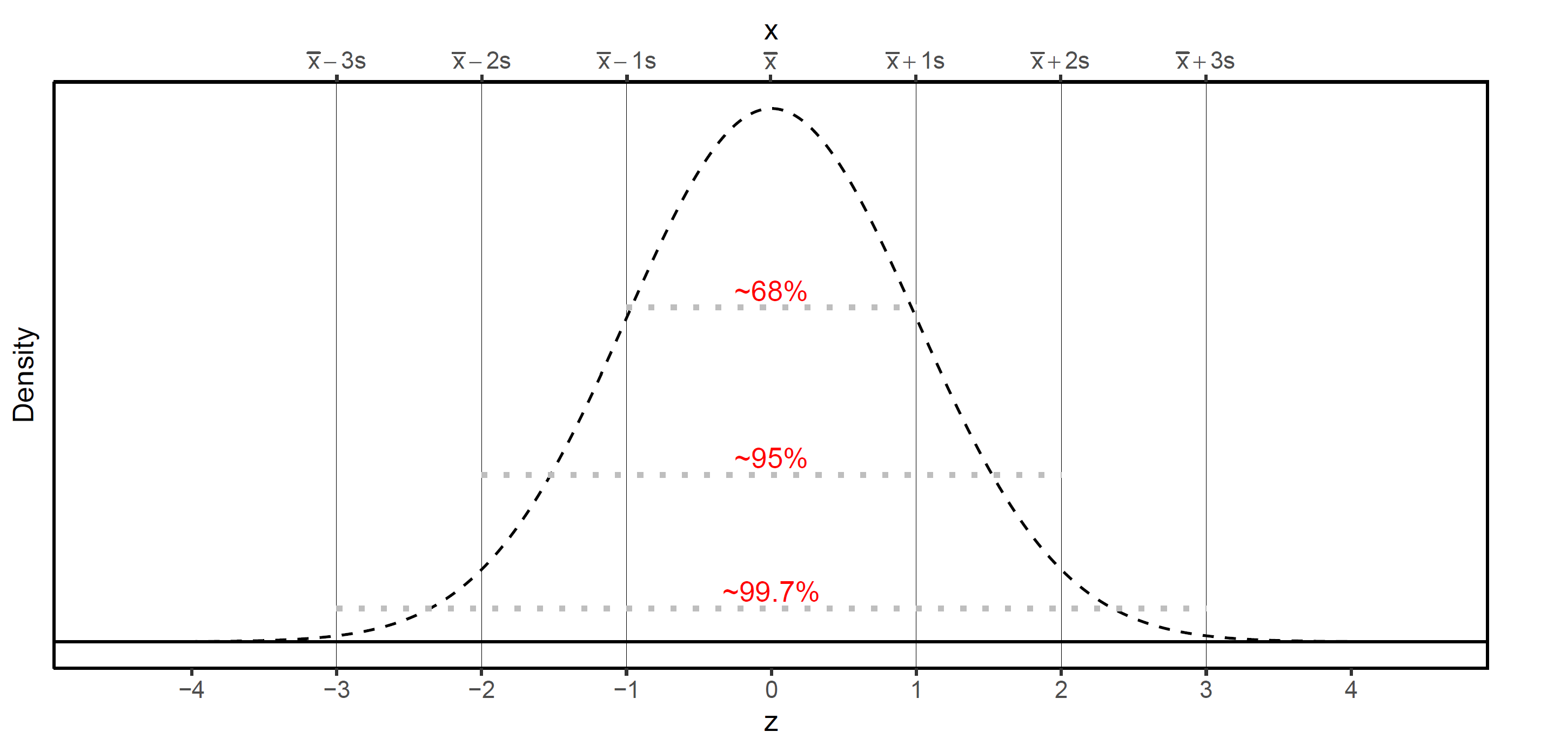
The Empirical Rule describes what portion of observations we can expect between one, two, and three standard deviations of the mean under the Gaussian (Normal) distribution. Specifically, the Empirical Rule states that we can expect 68% of observations within one standard deviation of the mean, 95% of observations within two standard deviations of the mean, 99.7% of observations within three standard deviations of the mean. This is depicted in the figure below.
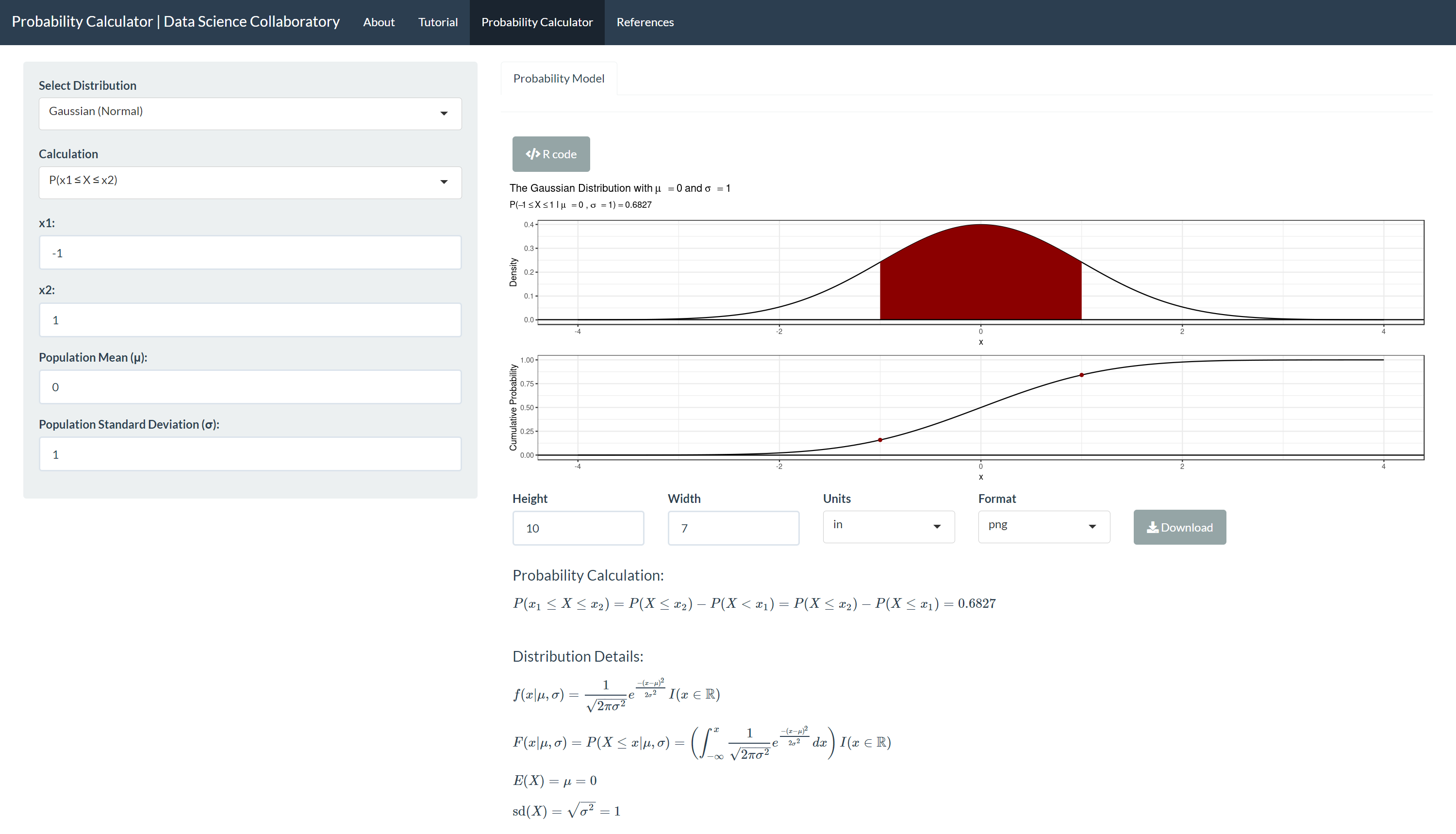
We can confirm this using the Probability Calculator. First, we show that 68% of observations are between -1 and 1 under a standard Gaussian (Normal) distribution where μ =0 and σ =1.
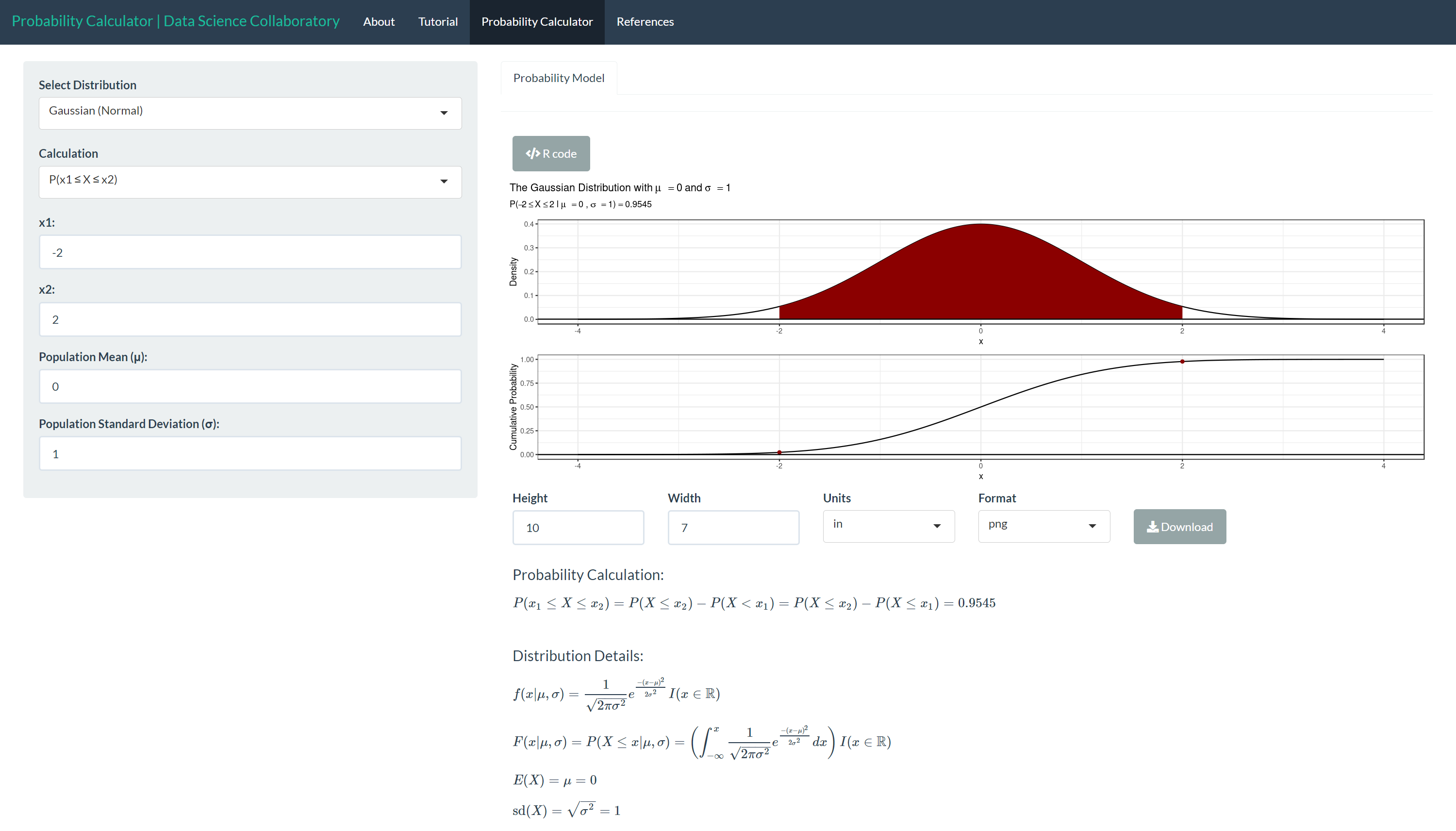
Next, we show that 68% of observations are between -2 and 2 under a standard Gaussian (Normal) distribution where μ =0 and σ =1.
Finally, we show that 68% of observations are between -3 and 3 under a standard Gaussian (Normal) distribution where μ =0 and σ =1.
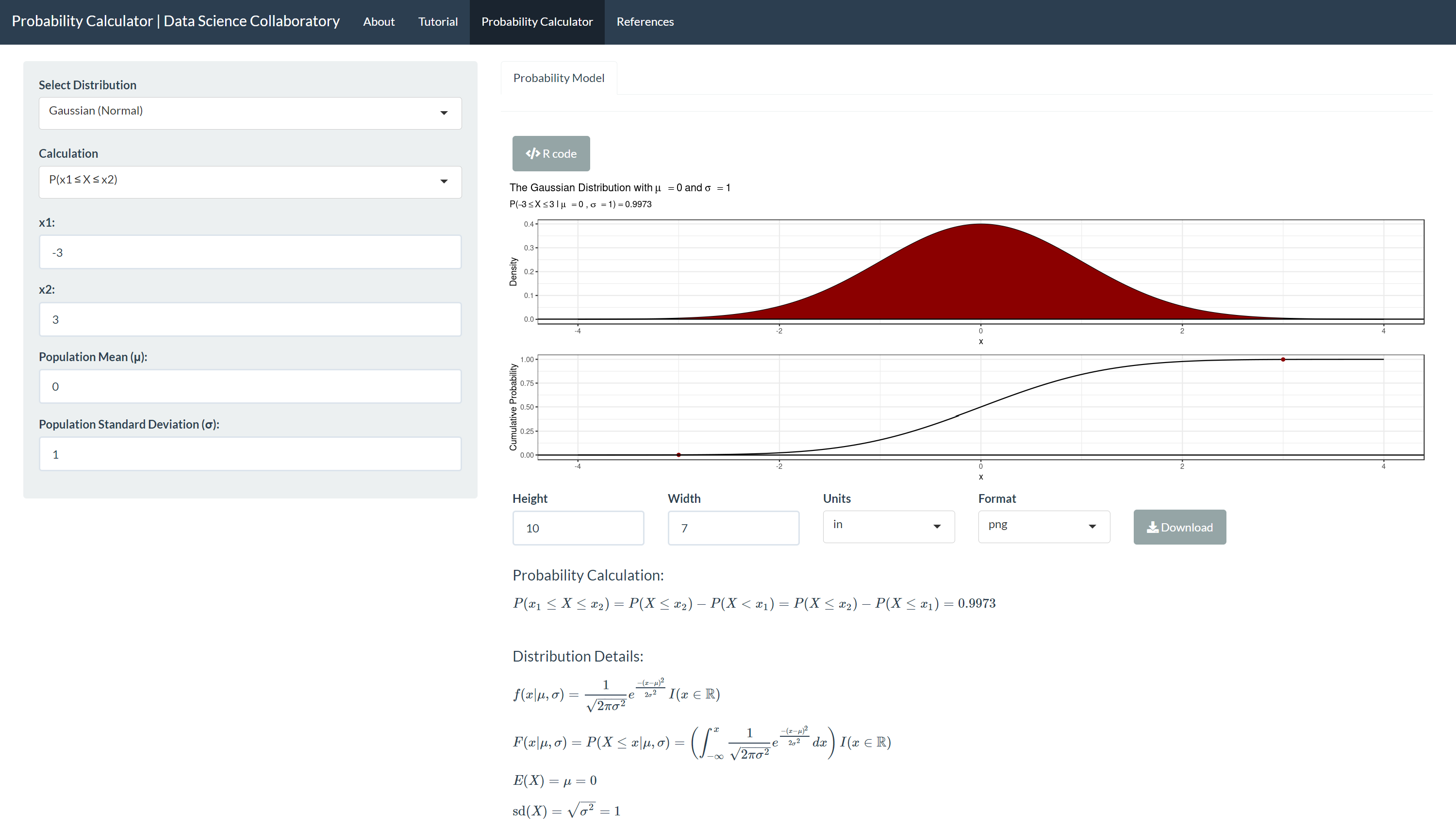
We have shown the Empirical Rule holds under the standard Gaussian (Normal) distribution. Note that this demonstration shows that there are only a small portion of observations that fall 'far' -- more than three standard deviations -- from the mean. You may also note that observations with a standardized observation or z-score less than -3 or more than 3 only occur 0.3% of the time; these rare observations are outliers.
References
Attali, Dean. 2021. Shinyjs: Easily Improve the User Experience of
Your Shiny Apps in Seconds. https://deanattali.com/shinyjs/.
Attali, Dean, and Tristan Edwards. 2021. Shinyalert: Easily Create
Pretty Popup Messages (Modals) in Shiny. https://github.com/daattali/shinyalert
https:// daattali.com/shiny/shinyalert-demo/.
Bailey, Eric. 2022. shinyBS: Twitter Bootstrap Components for
Shiny. https://ebailey78.github.io/shinyBS.
Chang, Winston. 2021. Shinythemes: Themes for Shiny. https://rstudio.github.io/shinythemes/.
Chang, Winston, Joe Cheng, JJ Allaire, Carson Sievert, Barret Schloerke,
Yihui Xie, Jeff Allen, Jonathan McPherson, Alan Dipert, and Barbara
Borges. 2022. Shiny: Web Application Framework for r. https://shiny.rstudio.com/.
Cheng, Joe, and Carson Sievert. 2021. Shinymeta: Export Domain Logic
from Shiny Using Meta-Programming. https://CRAN.R-project.org/package=shinymeta.
Dahl, David B., David Scott, Charles Roosen, Arni Magnusson, and
Jonathan Swinton. 2019. Xtable: Export Tables to LaTeX or HTML.
http://xtable.r-forge.r-project.org/.
Nijs, Vincent, Forest Fang, Trestle Technology, LLC, and Jeff Allen.
2022. shinyAce: Ace Editor Bindings for Shiny. https://CRAN.R-project.org/package=shinyAce.
Pedersen, Thomas Lin. 2022. Patchwork: The Composer of Plots.
https://CRAN.R-project.org/package=patchwork.
R Core Team. 2021. R: A Language and Environment for Statistical
Computing. Vienna, Austria: R Foundation for Statistical Computing.
https://www.R-project.org/.
Sali, Andras, and Dean Attali. 2020. Shinycssloaders: Add Loading
Animations to a Shiny Output While It’s Recalculating. https://github.com/daattali/shinycssloaders.
Wickham, Hadley. 2022. Tidyverse: Easily Install and Load the
Tidyverse. https://CRAN.R-project.org/package=tidyverse.
Wickham, Hadley, Mara Averick, Jennifer Bryan, Winston Chang, Lucy
D’Agostino McGowan, Romain François, Garrett Grolemund, et al. 2019.
“Welcome to the tidyverse.”
Journal of Open Source Software 4 (43): 1686. https://doi.org/10.21105/joss.01686.
Xie, Yihui. 2014. “Knitr: A Comprehensive Tool for Reproducible
Research in R.” In Implementing Reproducible
Computational Research, edited by Victoria Stodden, Friedrich
Leisch, and Roger D. Peng. Chapman; Hall/CRC. http://www.crcpress.com/product/isbn/ 9781466561595.
———. 2015. Dynamic Documents with R and Knitr. 2nd
ed. Boca Raton, Florida: Chapman; Hall/CRC. https://yihui.org/knitr/.
———. 2022. Knitr: A General-Purpose Package for Dynamic Report
Generation in r. https://yihui.org/knitr/.
Xie, Yihui, Joe Cheng, and Xianying Tan. 2022. DT: A Wrapper of the
JavaScript Library DataTables. https://github.com/rstudio/DT.